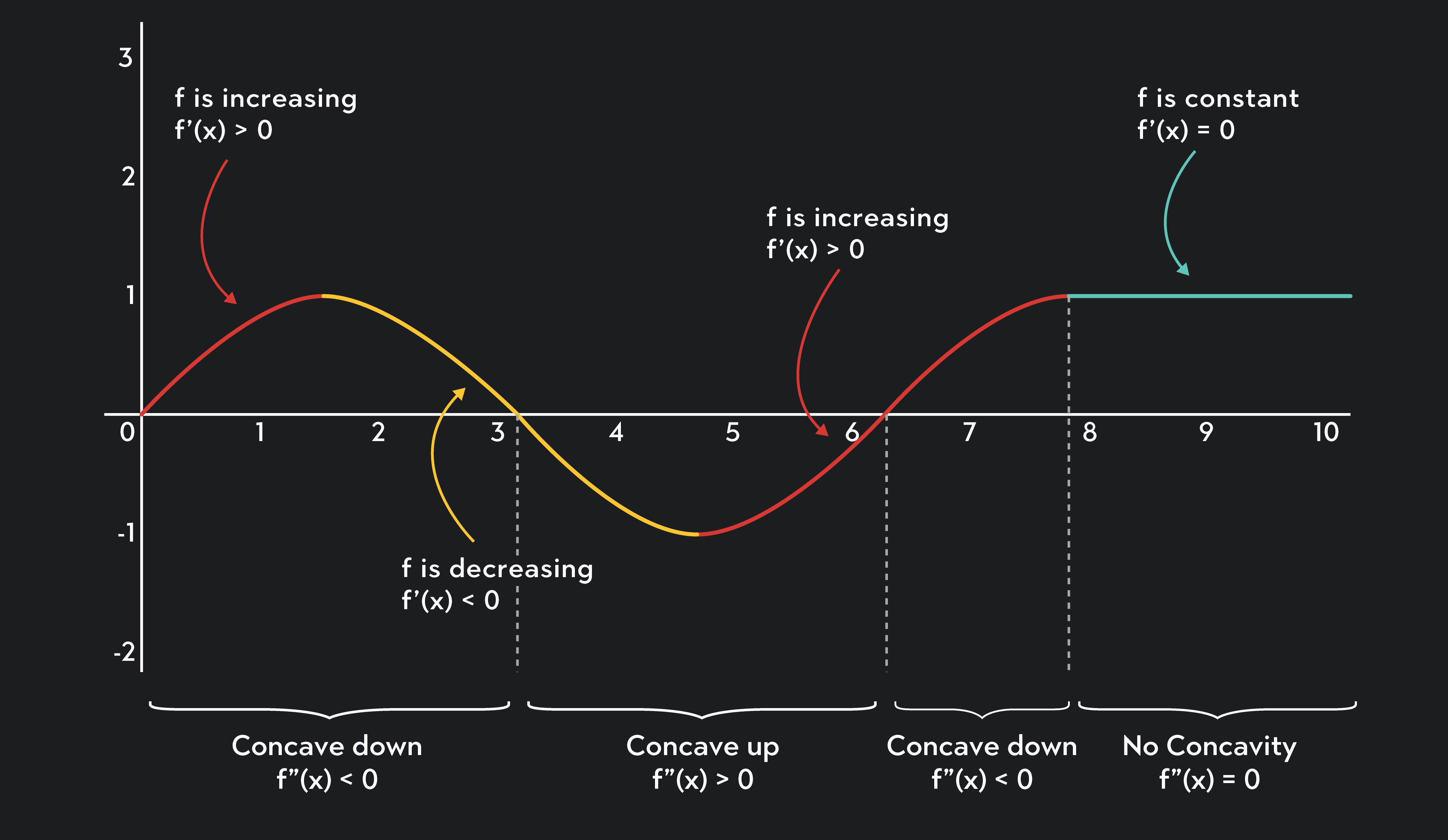
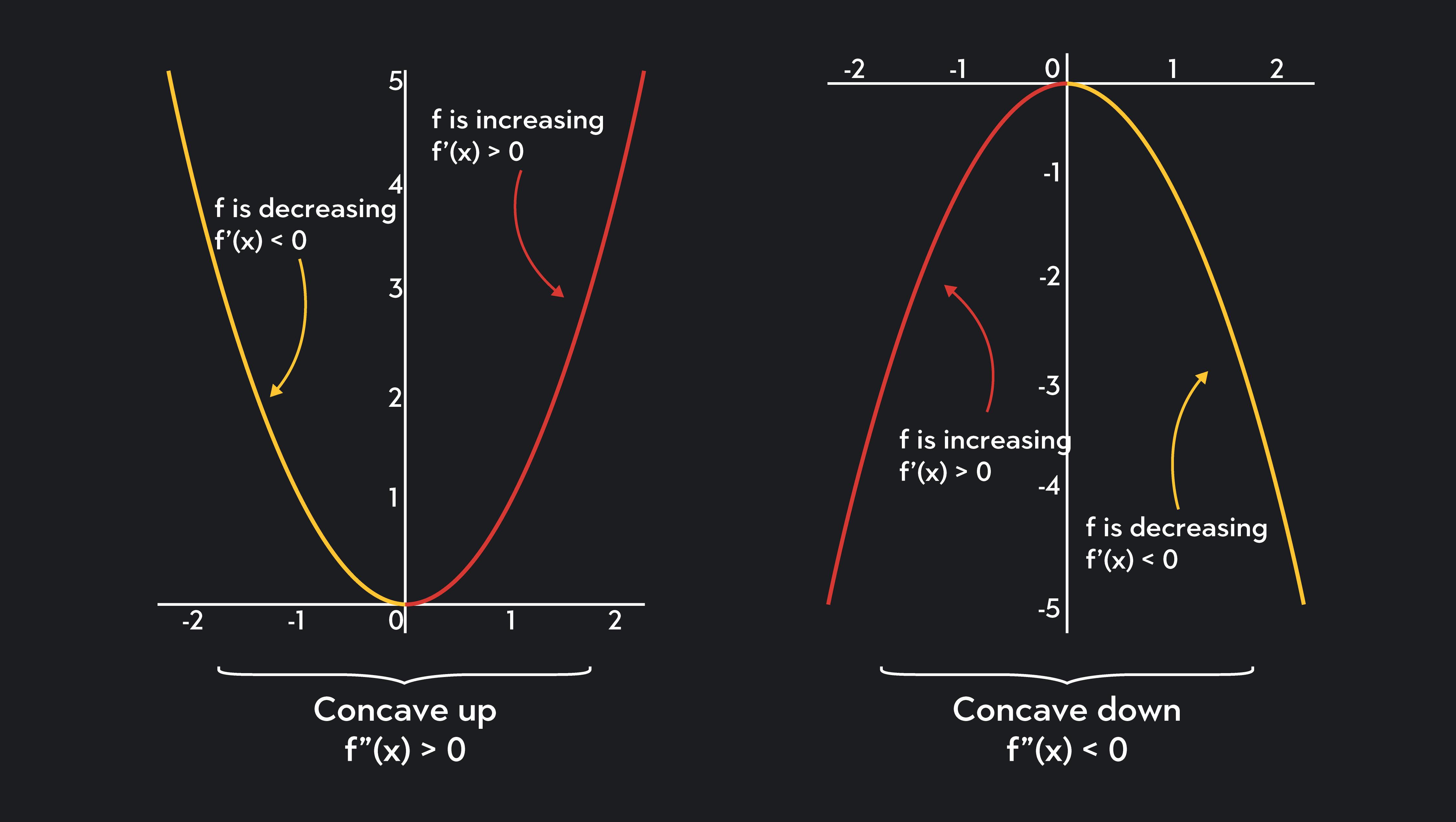
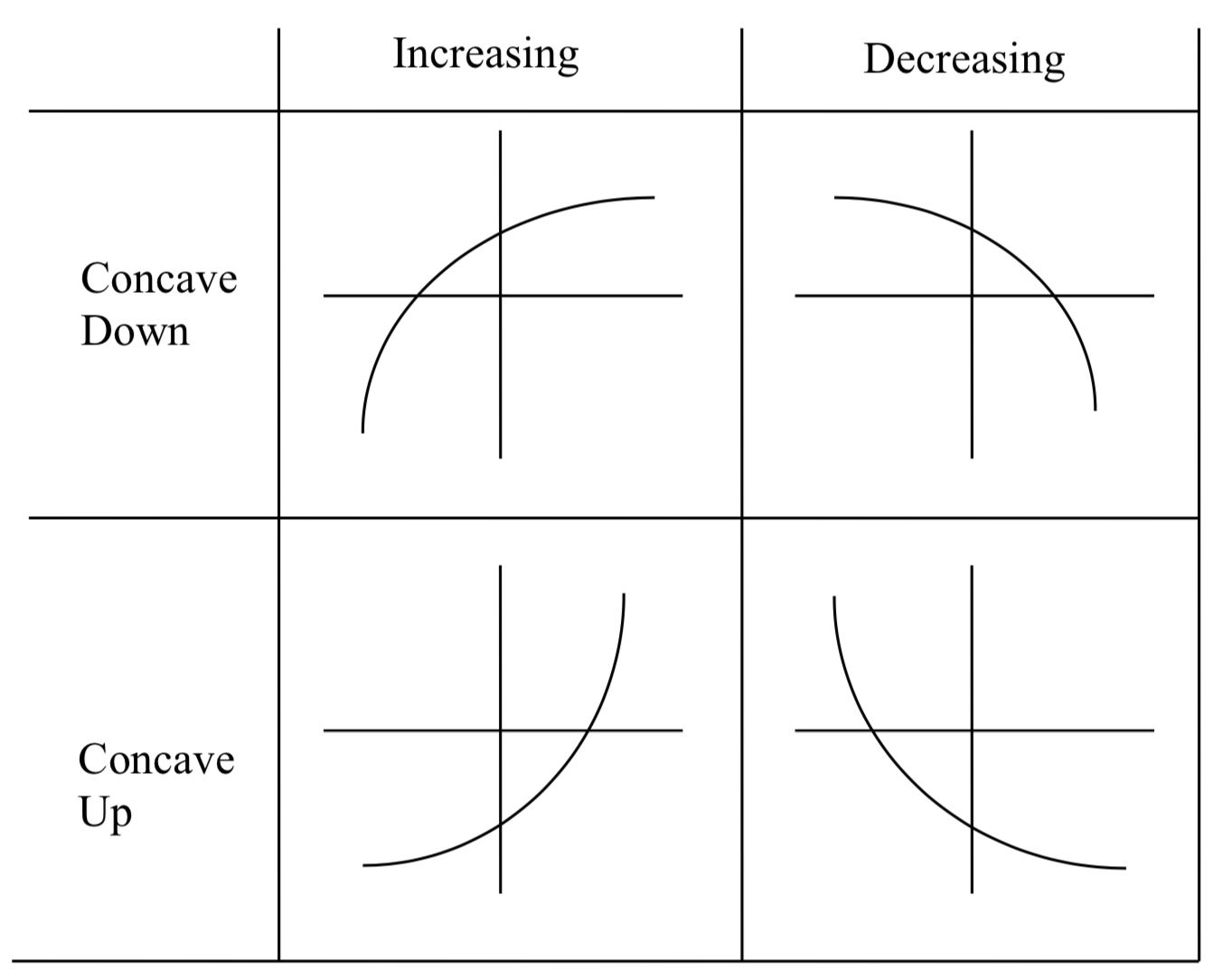
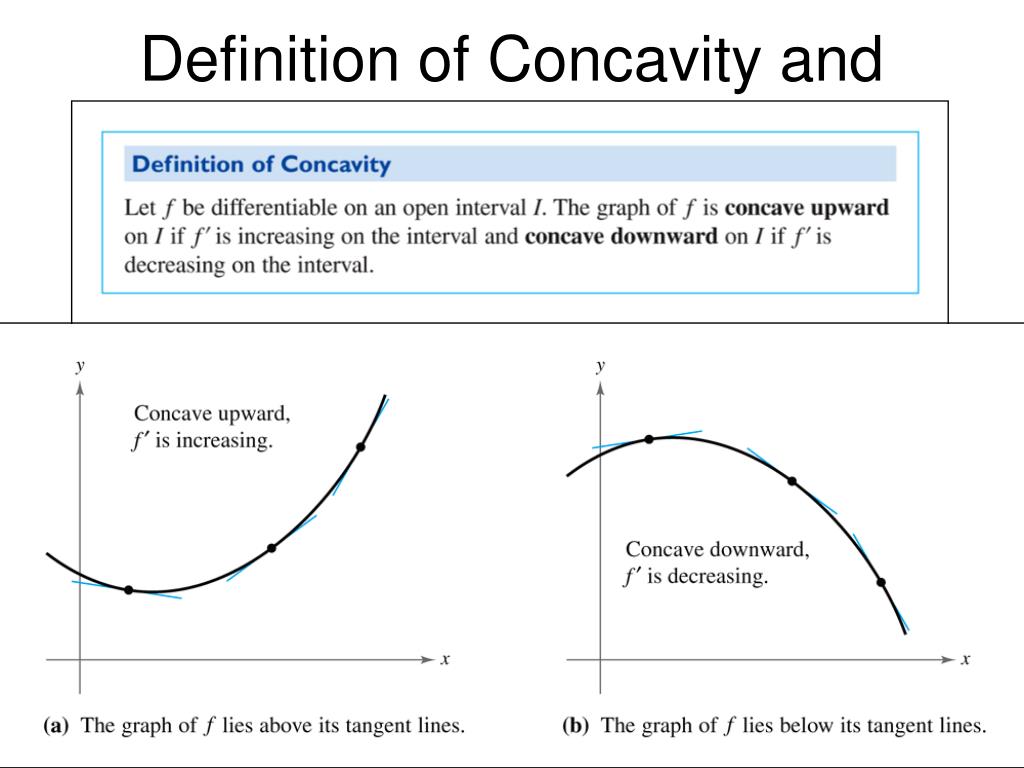
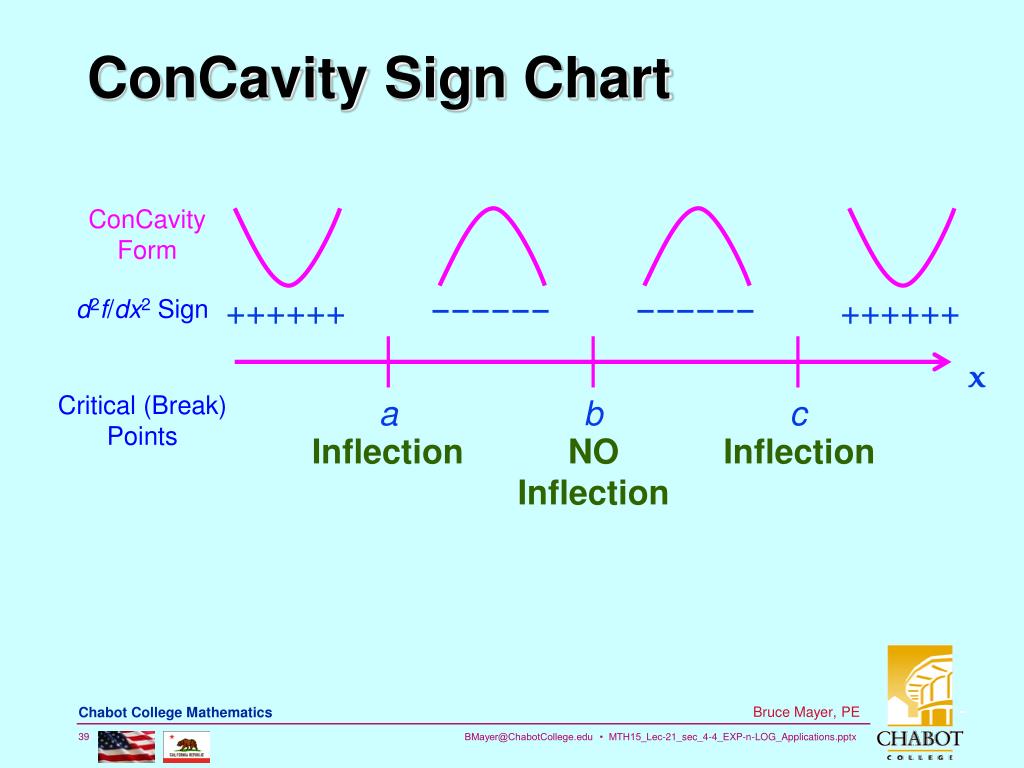
Concavity Chart
Concavity Chart - To find concavity of a function y = f (x), we will follow the procedure given below. This curvature is described as being concave up or concave down. Previously, concavity was defined using secant lines, which compare. Concavity in calculus refers to the direction in which a function curves. If the average rates are increasing on an interval then the function is concave up and if the average rates are decreasing on an interval then the. Find the first derivative f ' (x). Knowing about the graph’s concavity will also be helpful when sketching functions with. Concavity describes the shape of the curve. Definition concave up and concave down. The definition of the concavity of a graph is introduced along with inflection points. A function’s concavity describes how its graph bends—whether it curves upwards like a bowl or downwards like an arch. The graph of \ (f\) is. The graph of \ (f\) is concave up on \ (i\) if \ (f'\) is increasing. If a function is concave up, it curves upwards like a smile, and if it is concave down, it curves downwards like a frown. Examples, with detailed solutions, are used to clarify the concept of concavity. Concavity in calculus helps us predict the shape and behavior of a graph at critical intervals and points. The definition of the concavity of a graph is introduced along with inflection points. By equating the first derivative to 0, we will receive critical numbers. Let \ (f\) be differentiable on an interval \ (i\). If the average rates are increasing on an interval then the function is concave up and if the average rates are decreasing on an interval then the. Similarly, a function is concave down if its graph opens downward (figure 4.2.1b 4.2. If the average rates are increasing on an interval then the function is concave up and if the average rates are decreasing on an interval then the. The concavity of the graph of a function refers to the curvature of the graph over an interval; If. Generally, a concave up curve. Let \ (f\) be differentiable on an interval \ (i\). Graphically, a function is concave up if its graph is curved with the opening upward (figure 4.2.1a 4.2. Find the first derivative f ' (x). Concavity describes the shape of the curve. Concavity describes the shape of the curve. Concavity in calculus helps us predict the shape and behavior of a graph at critical intervals and points. This curvature is described as being concave up or concave down. Concavity suppose f(x) is differentiable on an open interval, i. Concavity in calculus refers to the direction in which a function curves. Concavity describes the shape of the curve. Previously, concavity was defined using secant lines, which compare. Find the first derivative f ' (x). Concavity in calculus refers to the direction in which a function curves. The definition of the concavity of a graph is introduced along with inflection points. A function’s concavity describes how its graph bends—whether it curves upwards like a bowl or downwards like an arch. Let \ (f\) be differentiable on an interval \ (i\). If the average rates are increasing on an interval then the function is concave up and if the average rates are decreasing on an interval then the. Knowing about the graph’s. Knowing about the graph’s concavity will also be helpful when sketching functions with. Let \ (f\) be differentiable on an interval \ (i\). Generally, a concave up curve. Similarly, a function is concave down if its graph opens downward (figure 4.2.1b 4.2. Definition concave up and concave down. By equating the first derivative to 0, we will receive critical numbers. This curvature is described as being concave up or concave down. Concavity in calculus refers to the direction in which a function curves. If the average rates are increasing on an interval then the function is concave up and if the average rates are decreasing on an interval. Concavity describes the shape of the curve. If a function is concave up, it curves upwards like a smile, and if it is concave down, it curves downwards like a frown. If f′(x) is increasing on i, then f(x) is concave up on i and if f′(x) is decreasing on i, then f(x) is concave down on i. Let \. Previously, concavity was defined using secant lines, which compare. Concavity describes the shape of the curve. Generally, a concave up curve. The concavity of the graph of a function refers to the curvature of the graph over an interval; If a function is concave up, it curves upwards like a smile, and if it is concave down, it curves downwards. The graph of \ (f\) is concave up on \ (i\) if \ (f'\) is increasing. Knowing about the graph’s concavity will also be helpful when sketching functions with. Examples, with detailed solutions, are used to clarify the concept of concavity. Concavity suppose f(x) is differentiable on an open interval, i. The concavity of the graph of a function refers. Concavity suppose f(x) is differentiable on an open interval, i. Concavity describes the shape of the curve. Examples, with detailed solutions, are used to clarify the concept of concavity. Similarly, a function is concave down if its graph opens downward (figure 4.2.1b 4.2. If a function is concave up, it curves upwards like a smile, and if it is concave down, it curves downwards like a frown. A function’s concavity describes how its graph bends—whether it curves upwards like a bowl or downwards like an arch. Find the first derivative f ' (x). The graph of \ (f\) is. Let \ (f\) be differentiable on an interval \ (i\). Concavity in calculus helps us predict the shape and behavior of a graph at critical intervals and points. This curvature is described as being concave up or concave down. The definition of the concavity of a graph is introduced along with inflection points. The graph of \ (f\) is concave up on \ (i\) if \ (f'\) is increasing. If f′(x) is increasing on i, then f(x) is concave up on i and if f′(x) is decreasing on i, then f(x) is concave down on i. Previously, concavity was defined using secant lines, which compare. Generally, a concave up curve.Concave Up and Concave Down Meaning and Examples Outlier
PPT Increasing/Decreasing Functions and Concavity PowerPoint Presentation ID2743916
Concave Up and Concave Down Meaning and Examples Outlier
1.4 Concavity Precalculus
1.3 Rates of Change and Behavior of Graphs Mathematics LibreTexts
Ex Concavity / Increasing / Decreasing Functions as Tables (Algebra Topic) YouTube
PPT CHAPTER 3 SECTION 3.4 CONCAVITY AND THE SECOND DERIVATIVE TEST PowerPoint Presentation
PPT Bruce Mayer, PE Licensed Electrical & Mechanical Engineer BMayerChabotCollege.edu
Using the 2nd Derivative Determining Concavity YouTube
Concave Down Definition & Graphs Lesson
By Equating The First Derivative To 0, We Will Receive Critical Numbers.
To Find Concavity Of A Function Y = F (X), We Will Follow The Procedure Given Below.
If The Average Rates Are Increasing On An Interval Then The Function Is Concave Up And If The Average Rates Are Decreasing On An Interval Then The.
Definition Concave Up And Concave Down.
Related Post: